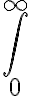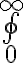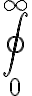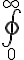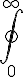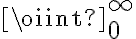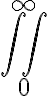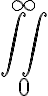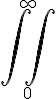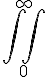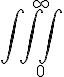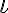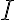Sfoglia il glossario usando questo indice
Caratteri speciali |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
TUTTI
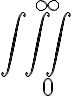
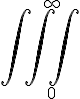
integrale - Sintassi generale per simboli con una sorta di limiti inferiori e superiori: \symbolname_{lowerexpression}^{upperexpression}
- In generale ci sono due modi in cui espressioni superiori ed inferiori possono essere posizionate: centrate sopra e sotto il simbolo o come apici e pedici.
Nel primo caso il nome del simbolo è preceduto dalla parola "big", nel secondo non c'è prefisso. - Es.: Sintassi per il simbolo di integrale:
$$\int_{0}^{\infty}$$ genera 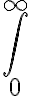
|
|
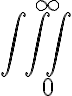
integrale di superficie $$\oiint_{0}^{\infty}$$ genera 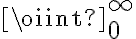 |
|
iota iota minuscolo $$\iota$$ genera 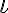
iota maiuscolo $$I$$ genra 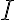 |
|
 Per la scrittura di formule matematiche sulla piattaforma Minerva si consiglia di adottare la notazione
Matematica Tex.
Per la scrittura di formule matematiche sulla piattaforma Minerva si consiglia di adottare la notazione
Matematica Tex.