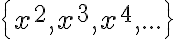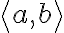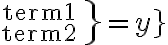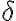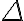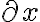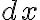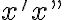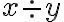Sfoglia il glossario usando questo indice
Caratteri speciali |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
TUTTI
alfa alfa minuscolo $$\alpha$$ genera 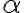
alfa maiuscolo $$A$$ genera 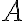 |
|
apici - Il carattere di comando "^" innesca la posizione apice delle seguenti espressioni.
- Per avere più caratteri in posizione apice usare le parentesi graffe {...}.
- Usare il comando di dimensionamento font per ottenere la grandezza desiderata.
Es.: $$x^2$$ genera 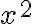 Es. con dimensioni caratteri specificate: $$x^{\small2}=a^{\small{m+2n}}$$ genera 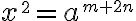 - Combinazione di caratteri apici e pedici.
Es.:$$A_{\small{i,j,k}}^{\small{-n+2}}$$ genera 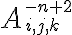 |
|
avviare il filtro Tex Per inserire un espressione matematica con la notazione Tex si deve racchiudere l'espessione tra due doppie $. La notazione sarà trasformata in una immagine gif. Per rendere visibile il codice Tex dell'espressione matematica usare due triple $ Esempio 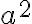 si ottiene scrivendo $$ a^2 $$ si ottiene scrivendo $$ a^2 $$ |
|
beta beta minuscolo $$\beta $$ genera 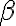
beta maiuscolo $$B$$ genera 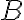 |
|
chi chi minuscola $$\chi$$ genera 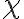
chi maiuscola $$X$$ genera 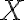 |
|
costanti - I numeri nelle formule sono interpretati come costanti e resi col font roman (non in corsivo), secondo una convenzione largamente usata.
Es.: $$f(x)=3a+x$$ genera 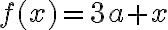 |
|
delta delta minuscolo $$\delta$$ genera 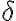
delta maiuscolo $$\Delta$$ genera 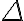 |
|
divisione $$x \div y$$ genera 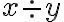 |
|
 Per la scrittura di formule matematiche sulla piattaforma Minerva si consiglia di adottare la notazione
Matematica Tex.
Per la scrittura di formule matematiche sulla piattaforma Minerva si consiglia di adottare la notazione
Matematica Tex. 
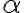
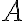
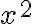
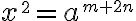
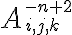
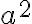
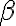
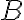
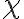
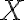
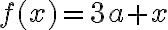
![\left[a^2+b^2~\right] \left[a^2+b^2~\right]](https://minerva.ic.cnr.it/filter/tex/pix.php/ad294afe2a577ffb993175209d64eb1d.gif)