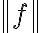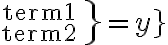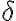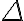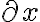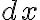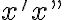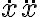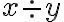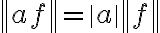Notazione matematica con LaTeX
 Per la scrittura di formule matematiche sulla piattaforma Minerva si consiglia di adottare la notazione
Matematica Tex.
Per la scrittura di formule matematiche sulla piattaforma Minerva si consiglia di adottare la notazione
Matematica Tex. 
Sfoglia il glossario usando questo indice
Caratteri speciali | A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | TUTTI
D |
|---|
delta | |
derivate | |
divisione | |
doppia linea verticale (norma) | |
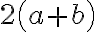
![\left[a^2+b^2~\right] \left[a^2+b^2~\right]](https://minerva.ic.cnr.it/filter/tex/pix.php/ad294afe2a577ffb993175209d64eb1d.gif)